Линейная регрессия – один из важнейших статисических методов, позволяющих прогнозировать значения зависимой переменной, используя значения одной или нескольких независимых переменных.
Построить линию регрессии с помощью Python можно несколькими способами, каждый из которых имеет свои плюсы и минусы, например можно воспользоваться инструментарием библиотеки scikit-learn, методом scipy.polyfit или numpy.polyfit.
В данной статье рассматривается один из вариантов построения линии регрессии с помощью функции stats.lingress стандартной библиотеки scipy.

Stats.lingress – функция, оптимизированная для вычисления линейной регрессии методом наименьших квадратов на вход которой можно подать только два набора измерений. С помощью этой функции вы не сможете получить обобщенную линейную модель или рассчитать многовариантную регрессию, но при всех вышеперечисленных минусах данная функция ‑ один самых быстрых методов расчета простой линейной регрессии, среди других вариантов, предлагаемых python. Так что, если у вас большой объем данных – использование stats.lingress позволит сэкономить на времени вычислений.
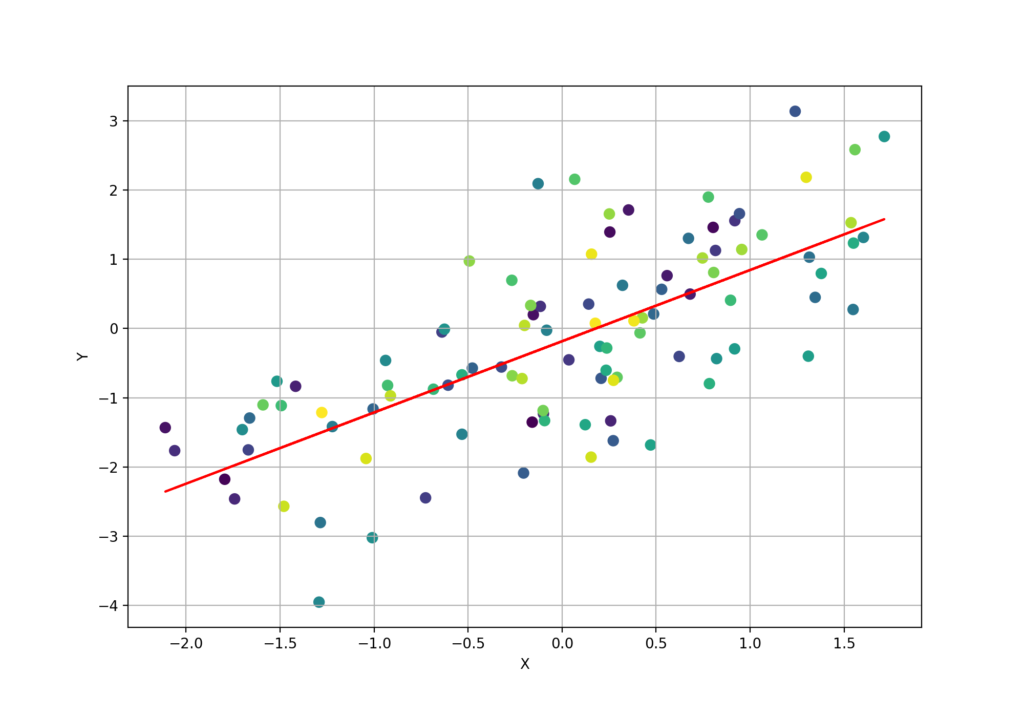
В качестве примера сгенерируем два набора измерений, один из которых зависит от другого:
from scipy import stats import numpy as np import matplotlib.pyplot as plt # генерируем данные n = 100 x = np.random.randn(n) y = x+np.random.randn(n)
Если данные будут анализироваться с учетом последовательности их регистрации (скажем данные были записаны с определенным шагом по времени), можно добавить еще одну переменную к нашему набору данных
numb=np.arange(0,n,1)
Собственно, сам расчет коэффициентов для линии регрессии и ее статистических показателей выражается следующей строкой кода:
slope, intercept, r_value, p_value, std_err = stats.linregress(x,y)
Для вывода линии регрессии на кроссплоте добавляем:
line = slope*x+intercept
Следующим шагом настраиваем визуализацию, где помимо прочего выведем значение R2
Параметр r_value можно использовать в качестве количественной оценки того, насколько хорошо расчитанная нами линия регрессии соответствует данным. Значение R2 будет находится в интервале от 0 до 1, соответственно, чем ближе это значение к единице, тем более достоверна будет оценка, если мы воспользуемся расчитанным уравнением регрессии для прогнозирования
fig = plt.figure(figsize=(10,7))
ax = plt.subplot(111)
plt.scatter(x,y, s=50, c=numb)
plt.plot(x, line, 'r', label='y={:.2f}x+{:.2f}'.format(slope,intercept))
plt.plot([], [], ' ', label='R_sq = '+'{:.2f}'.format(r_value**2))
plt.grid(True)
plt.legend(fontsize=12)
plt.colorbar()
plt.xlabel('X')
plt.ylabel('Y')
plt.show()Весь код целиком можно забрать тут:
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
# генерируем данные
n = 100
x = np.random.randn(n)
y = x+np.random.randn(n)
numb=np.arange(0,n,1)
#линия регрессии
slope, intercept, r_value, p_value, std_err = stats.linregress(x,y)
line = slope*x+intercept
#создание кроссплота
fig = plt.figure(figsize=(10,7))
ax = plt.subplot(111)
plt.scatter(x,y, s=50, c=numb)
plt.plot(x, line, 'r', label='y={:.2f}x+{:.2f}'.format(slope,intercept))
plt.plot([], [], ' ', label='R_sq = '+'{:.2f}'.format(r_value**2))
plt.grid(True)
plt.legend(fontsize=12)
plt.colorbar()
plt.xlabel('X')
plt.ylabel('Y')
plt.show()